Изображение - это двумерный сигнал, предназначенный для зрительного восприятия человеком.
Изображения создаются изображающими системами. Назначение этих систем - сделать доступной для визуального восприятия информацию, которая непосредственно не может быть воспринята зрением.
Можно выделить следующие категории задач обработки изображений:
- коррекция изображающих систем;
- препарирование изображений;
- визуализация информации;
- измерения на изображениях;
- кодирование изображений;
- моделирование изображающих систем.
Коррекция изображающих систем - это обработка видеосигнала в реальной изображающей системе, направленная на получение изображения, соответствующего идеальной изображающей системе. Примером коррекции может служить повышение чёткости расфокусированных изображений, устранение смаза, подавление шумов.
Для отдельных задач могут требоваться дополнительные преобразования сигнала, облегчающие визуальный анализ путём подчёркивания одних особенностей и деталей изображений и устранения других, изменения пространственных соотношений, измерения и визуализации количественных характеристик и т.д. Такие преобразования, являющиеся инструментом визуального анализа, называются препарированием изображений. Примерами препарирования могут служить: построение изофот, оконтуривание, передача изображений в псевдоцевтах и т.д.
Под визуализацией информации понимают обработку сигналов для представления их в виде изображений с целью последующей визуальной интерпретации.
Автоматическую обработку сигналов, которые будучи представлены в виде изображений, могли бы анализироваться визуально, называют измерениями на изображениях. Это, например, автоматическое измерение размеров и пространственного расположения объектов, их обнаружение, классификация.
Кодирование изображений - это преобразования видеосигнала, необходимые для его запоминания в запоминающих устройствах или передачи по каналам связи в цифровой форме.
К моделированию изображающих систем относится категория задач обработки изображений, которые решаются при создании и исследовании новых типов систем.
Чаще всего в качестве математических моделей сигналов используются скалярные функции. Но иногда приходится прибегать к более сложным моделям - комплексным и векторным функциям. Например, для описания электромагнитного поля как сигнала удобно использовать комплексные функции, для описания цветных изображений - трёхкомпонентные векторные функции.
Если сигнал и его аргументы принимают любые значения на отрезке или на бесконечной оси, то есть несчётное множество значений, то сигнал называют непрерывным, или аналоговым. Сигнал, аргументы которого принимают только счётное множество значений, называется квантованным. Дискретные квантованные сигналы называются цифровыми.
Двумерный интервал - период периодического сигнала - это плоская фигура, а не отрезок.
С точки зрения математического описания сигналов различают детерминированные и вероятностные описания. При детерминированном описании сигналы рассматриваются изолированно, независимо друг от друга, и считается, что значение сигнала задано в каждой точке, где он определён. При использовании вероятностного описания сигналы рассматриваются как функции или реализации из некоторого ансамбля сигналов, и математическое описание строится не для каждого отдельного сигнала, а для ансамбля в целом.
В цифровой обработке изображений цифровые сигналы это искусственные объекты, являющиеся результатом преобразования непрерывных сигналов.
Математически преобразования сигналов удобно трактовать как отображения в пространстве сигналов. В общем случае для описания такого отображения нужно задать все возможные пары входных и выходных сигналов, то есть упорядочить все пары вход-выход. Но это неконструктивная задача.
Приходится ограничиваться "иерархическими" описаниями, то есть представлять желаемые преобразования как достаточно простую совокупность "элементарных" преобразований, каждое из которых может быть описано с помощью небольшого подмножества из всех возможных пар вход-выход.
Важнейшими из таких "элементарных" преобразований являются так называемые линейные преобразования и поэлементные нелинейные преобразования.
Линейные преобразования определяются на линейном пространстве и обладают следующими свойствами:
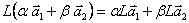
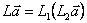
Физическим эквивалентом произведения является последовательное (каскадное) соединение блоков, реализующих операторы - сомножители.
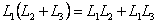
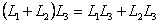
Если оператор L осуществляет взаимно-однозначное отображение области определения, то существует обратный оператор L-1, такой что:
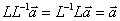
Нелинейные поэлементные преобразования - взятых по отдельности коэффициентов представления сигнала по заданному базису, причём закон преобразования каждого элемента зависит только от его номера и не зависит от значений других коэффициентов.
Линейные преобразования характерны тем, что их результат может быть описан с помощью результатов преобразования только базисных функций. Для этого требуется задать N векторов, а в случае, если векторы-базисы являются так называемыми собственными векторами преобразования, то N чисел.
Нелинейные поэлементные преобразования могут быть описаны M числами-результатами нелинейных преобразований коэффициента представления сигналов по заданному базису. Таким образом, для определения нелинейного поэлементного преобразования достаточно задать таблицу из M чисел.
Представление линейных преобразований по отношению к дискретным базисам:
1) с помощью вектор-откликов;
2) матричное представление;
3) представление операторов с помощью их собственных функций и собственных значений.
Представление операторов по отношению к непрерывным базисам:
1) описание с помощью импульсной реакции (импульсной реакцией называется отклик оператора на δ-функцию);
2) описание с помощью частотной характеристики (отклик оператора на базисную экспоненту);
3) описание при разных базисах входных и выходных сигналов;
4) описание с помощью собственных функций.
В теории сигналов линейные операторы часто называют линейными фильтрами.
Дискретизация и квантование сигналов
Преобразование аналогового сигнала в цифровой состоит в отображении пространства аналоговых сигналов в конечное множество сигналов, то есть пространство сигналов разбивается на конечное множество подпространств, и в каждом подпространстве выбирается один принадлежащий ему сигнал-представитель так, чтобы все остальные сигналы данного подпространства можно было в пределах заданной степени точности заменить этим сигналом-представителем. Подпространства перенумеровываются, и, таким образом, каждому аналоговому сигналу в пространстве сигналов, разбитом на ячейки, или области эквивалентности, может быть поставлено в соответствие число - номер сигнала представителя. Такое разбиение пространства сигналов называется обобщённым квантованием.
Важным вопросом обобщённого квантования является объём получающегося цифрового представления. Этот объём можно оценить как количество дискретных квантованных сигналов-представителей. От него непосредственно зависит сложность цифровой системы обработки.
Наиболее общий метод оценки объёма дискретного представления даёт теория информации на основе статистического описания сигналов и их преобразований. В соответствии с теоретико-информационной трактовкой каждому элементу объёма пространства сигналов приписывается некоторая вероятностная мера - вероятность того, что в массе реализаций (экспериментов, наблюдений и т.п.) встретятся принадлежащие ему сигналы.
Точность воспроизведения сигналов также трактуется статистически как среднее значение некоторого расстояния между сигналами в метрике, определяемой получателем сигналов и особенностями их обработки.
Обобщённое квантование обычно трудно реализовать как единую процедуру. Поэтому на практике при преобразовании непрерывных сигналов в цифровую форму прибегают к двухступенчатой процедуре дискретизации и поэлементному квантованию.
Дискретизация - это замена непрерывного сигнала последовательностью чисел, являющихся представлением этого сигнала по какому-либо ортонормированному базису. В случае, если данный сигнал не является элементом линейного пространства, натянутого на этот базис, отыскивается такой сигнал из этого пространства, который в некотором (специально оговоренном для каждой задачи!) смысле является наилучшим приближением данного сигнала, и затем уже отыскивается представление полученного аппроксимирующего сигнала. Базис линейного пространства может выбираться исходя из удобной физической реализации, точности аппроксимации и т.п.
Поэлементное квантование - это квантование по отдельности каждого из чисел {ак}, представляющих данный сигнал по заданному базису, то есть замена непрерывной (бесконечной) шкалы значений {а} дискретной и конечной.
Дискретизация относится к классу линейных преобразований сигнала, поэлементное квантование - к классу поэлементных нелинейных. Задача оптимального квантования сводится к оптимальному выбору системы базисных функций и оптимальному расположению шкалы квантования по координатным осям.
Самый распространённый способ дискретизации сигналов основывается на теореме отсчётов (теореме Котельникова).
Дискретизацию двумерных сигналов и изображений чаще всего основывают на теореме отсчётов, обобщённой на двумерный случай, поскольку во всех практических задачах можно считать, что спектр изображений отличен от нуля только на ограниченном участке частотной плоскости.
В практике цифровой обработки изображений и двумерных сигналов в настоящее время в основном используется простая дискретизация по прямоугольному растру как наиболее универсальная и лучше отвечающая одномерной структуре вычислительных машин и цифровых процессоров, используемых для обработки. Гескагональный растр используется в цветном телевидении и полиграфии. Другие виды косоугольного растра иногда используются в специальных цифровых телевизионных системах.
При обработке изображений используются как одномерные, так и двумерные линейные преобразования. Цифровая реализация этих преобразований называется цифровой фильтрацией. Способы цифровой фильтрации двумерных сигналов, основанные на представлении сигналов и импульсных реакций фильтров по теореме отсчётов, называются фильтрацией в пространственной области. Фильтрация сигналов может быть осуществлена путём преобразования их спектров (фильтрация в частотной области).
Одно из важнейших применений дискретных преобразований Фурье - вычисление с их помощью цифровой свёртки сигналов.
Дискретные преобразования Фурье являются удобным средством для нахождения незаданных промежуточных (то есть расположенных между заданными) отсчётов сигналов по его заданным отсчётам (интерполяции сигналов).
При определении требований к способу квантования непрерывных сигналов необходимо учитывать, что реальные датчики непрерывного видеосигнала и устройства воспроизведения изображений обладают собственными шумами, в результате чего отсутствует абсолютно точное соответствие между сигналом и объектом изучения. При расчёте оптимального нелинейного предыскажения при квантовании можно считать, что эти шумы, пересчитанные на вход равномерно квантующего устройства, аддитивно складываются с шумом квантования.
Важной особенностью взаимодействия этих двух видов искажений является рандомизация шума квантования, разрушение его корреляционных связей с квантуемым сигналом. В результате требования к допустимой величине шума квантования могут быть несколько снижены. Так, например, случайный шум датчика видеосигнала разрушает ложные контуры при грубом квантовании яркости изображения, уменьшая тем самым их заметность. На этом основан один из способов сокращённого описания изображений, заключающийся в том, что к видеосигналу перед грубым квантованием добавляется псевдослучайный шум с независимыми отсчётами, а при восстановлении изображения этот шум вычитается из квантованного видеосигнала. Аналогичный способ может использоваться и при повышении контраста изображений при цифровой обработке.
Существует некоторое оптимальное соотношение между этими видами шумов, зависящее от свойств квантуемого сигнала и содержания решаемой задачи. В большинстве случаев случайный шум датчика и синтезатора должен иметь примерно те же интенсивность (дисперсию), что и шум квантования.
Дискретное представление сигналов при цифровой обработке чаще всего основывают на теореме отсчётов, рассматривая сигналы как функции с ограниченным спектром Фурье.
Возможность представления импульсивной реакции двумерного фильтра в разделимой форме в большой степени зависит от выбора системы координат. Выбор системы координат при обработке изображений важен также с точки зрения возможности рассматривать фильтры как инвариантные к сдвигу, или как пространственно-однородные. В ряде случаев фильтр можно сделать пространственно-однородным, если выбрать специальную систему координат с нелинейной шкалой по координатам.
Представление импульсной реакции фильтра в виде суммы импульсных реакций более простого вида соответствует тому, что фильтрация сигнала осуществляется параллельно несколькими фильтрами и результаты фильтрации складываются (параллельно-каскадное представление).
Подобно дискретному преобразованию Фурье можно рассматривать дискретное преобразование Уолша как дискретный аналог непрерывного преобразования сигнала по базису, составленному из функций Уолша. Существует три версии этого преобразования, отличающиеся способом упорядочивания базисных функций, составляющих ядро преобразования: преобразование Уолша-Адамара, преобразование Пэли, преобразование Уолша. Все они определены на последовательностях, количество членов которых равно целой степени 2.
Матрицы преобразований Уолша являются симметрическими, то есть не меняющимися при транспонировании, и ортогональными, так как они обратные самим себе. Таким образом, преобразование Уолша, также как и дискретное преобразование Фурье, относятся к классу унитарных преобразований.
Применения унитарных преобразований в обработке изображений можно разбить на три группы:
1) кодирование изображений;
2) выделение признаков для препарирования и распознавания изображений;
3)обобщённая фильтрация.
Простейшей и в то же время одной из важнейших статистических характеристик сигналов является распределение вероятностей их значений. Для цифровых сигналов можно говорить о частоте, с которой встречаются их отдельные значения. Эта частота как функция значений сигнала называется гистограммой распределения значений.
Гистограмма, описывающая частоту появления значений отдельных отсчётов сигнала независимо от значений других отсчётов, называется одномерной, или гистограммой одномерного распределения. Гистограмма, характеризующая частоту совместного появления значений нескольких отсчётов сигнала, называют многомерной, или гистограммой многомерного распределения.
Гистограмма может использоваться как характеристика не только всего наблюдаемого изображения, но и отдельных его участков или фрагментов. В этом случае она называется локальной.
Гистограммы, измеренные по небольшим фрагментам изображений, обычно бывают довольно изрезанными функциями. При увеличении объёма измерений гистограмма, как правило, сглаживается. Однако иногда необходимо получить сглаженную гистограмму при малом объёме измерений. наиболее употребительны три метода сглаживания:
1) ступенчатое сглаживание (диапазон значений аргумента гистограммы разбивается на небольшое число интервалов, и значения гистограммы внутри каждого интервала заменяются средним значением по интервалу);
2) сглаживание скользящим суммированием;
3) сглаживание с помощью ортогональных преобразований (представляет особый интерес для многомерных распределений, если ступенчатое сглаживание нежелательно).
Для описания случайных воздействий на сигнал в изображающих системах пользуются моделями аддитивного, импульсного и мультипликативного шума.
Модель аддитивного шума используется тогда, когда сигнал на входе системы или на каком-либо промежуточном этапе его преобразования может рассматриваться как сумма полезного сигнала и некоторого случайного сигнала (шума).
Если действие шума сказывается не на всей протяжённости сигнала, а только на случайно расположенных точках, где значение сигнала заменяется случайной величиной, шум называется импульсным.
Мультипликативная модель применяется тогда, когда можно считать, что полезный сигнал умножается на случайный сигнал.
Линейные и нелинейные искажения также могут носить случайный характер. Тогда они описываются как преобразования, параметры которых являются случайными величинами или функциями.
Примером амплитудной коррекции может служить повышение контраста изображений. К повышению контраста прибегают тогда, когда цифровой видеосигнал занимает по тем или иным причинам только часть отведённого ему диапазона значений.
Введение фиктивных уровней квантования разрушает ложные контуры.
Статистические свойства импульсных помех резко отличаются от статистических свойств изображений. Для изображений характерны плавные, небольшие изменения значений видеосигнала от элемента к элементу, а быстрые, скачкообразные изменения редки и образуют протяжённые контуры. Импульсивные же помехи представляют собой значительные по величине одиночные изолированные выбросы.
Благодаря такому резкому отличию помех от изображений алгоритм фильтрации импульсных помех оказывается весьма простым. Он состоит из двух операций: обнаружения искажённых элементов изображения и исправления значения видеосигнала в этих элементах.
Диалоговый режим обработки обеспечивают дисплеи и дисплейные процессоры. Основное назначение дисплея - воспроизведение высококачественного чёрно-белого или цветного изображения и всей сопутствующей служебной алфавитно-цифровой и графической информации в форме, удобной для непосредственного визуального наблюдения, и в реальном времени, то есть так, чтобы воспроизведение изображения не замедляло диалог.
| 
