Под изображением понимается информация, организованная в виде некоторой квадратной числовой матрицы размером от 214 до 218, записанной на какой-либо машинный носитель и воспроизводящей свойства изображаемого объекта (сцены) и деформации, которые связаны со способом и процессом получения изображения.
Под обработкой изображения понимается применение к нему системы преобразований, приводящих изображение к виду, удобному для анализа или улучшающему его качество.
Под анализом изображения понимается применение к нему системы преобразований, обеспечивающей извлечение из изображения полезной информации о свойствах изображаемого объекта или процесса.
При работе с изображениями необходимо разрешать задачи, возникающие в связи с тремя основными проблемами:
1) описанием (моделированием) изображений;
2) разработкой и выбором математических средств обработки и анализа изображений;
3) аппаратной реализации математических методов работы с изображениями.
Контраст играет существенную роль в обработке изображений, поскольку часто именно им определяется качество "картинки". Цвет служит полезным признаком для разделения отдельных частей изображения, улучшающим одновременно его эстетические качества. Форма (очертания) представляет группу признаков, которые используются для распознавания объектов, содержащихся в изображении, с учётом его геометрических свойств. Группа текстурных признаков широко используется при отнесении изображения как отдельного объекта распознавания к некоторому классу и для интерпретации результатов решения задачи распознавания.
При распознавании (то есть при формализации изображения как объекта распознавания) "содержание" ("состав") изображения характеризуется информацией трёх типов:
1) идентифицируемые объекты с хорошо определённой структурой;
2) идентифицируемые объекты с плохо определённой структурой ("нечёткие" образы);
3) неидентифицируемые объекты.
Таким образом, в процессе анализа изображения должна использоваться информация, отражающая механизм формирования образа, то есть как изображения в целом, так и объектов, на нём представленных. Учёт структуры изображений сводится к определению того, какие подызображения (объекты) можно выделить на изображении, насколько они могут или должны быть элементарны и в каких отношениях пребывают эти объекты и элементы. Следовательно, в основе ввода структурной информации в описание объектов распознавания лежат изучение и использование структур отношений элементов, составляющих изображение. Реализуется этот метод при помощи построения модели изображения в виде иерархической структуры более простых объектов. В результате удаётся в явном виде представлять и использовать иерархическую структурную информацию, содержащуюся в изображении: изображение описывается через некоторую систему объектов, каждый объект описывается с помощью более простых объектов, последние снова описываются с помощью ещё более простых объектов и т.д.
При введении структурной информации в процессе распознавания используется то обстоятельство, что такая информация представляет свойственную реальному миру регулярность, проявляющуюся в возникновении разного рода упорядоченностей и структур. Обращение к комбинаторным регулярным структурам позволяет, оперируя весьма ограниченным числом непроизводных элементов и ограниченным набором правил комбинирования, с помощью неограниченного их применения к исходным непроизводным элементам и результатам применения отдельных комбинаторных преобразований получать практически неограниченное разнообразие описаний.
Задача машинной графики - воспроизведение изображений в тех случаях, когда исходной является информация неизобразительной природы.
Обработка изображений связана с решением таких задач, в которых и входные и выходные данные являются изображениями (может возникнуть даже задача построения нового изображения по набору других изображений, как это требуется при синтезе изображений поперечных сечений тела человека по рентгенограммам, соответствующим боковым проекциям).
Задачей распознавания изображений является применение методов, позволяющих либо получить некоторое описание изображения, поданного на вход системы, либо отнести это изображение к некоторому определённому классу. Распознавание зрительных образов представляет собой, в некотором смысле. обратную задачу машинной графики. Процедура распознавания применяется к некоторому изображению и обеспечивает преобразование его в некоторое абстрактное описание: набор чисел, цепочку символов или граф.
Автоматизация медицинской диагностики связана с обнаружением на рентгенограммах или иных изображениях медицинских объектов отклонений от нормы определённого вида.
Характеризуя плотность размещения выборочных точек, говорят о пространственном разрешении, а характеризуя точность представления результатов указанных измерений - о тоновом (или цветовом) разрешении.
Нелинейная фильтрация изображений
К фильтрам, применение которых обеспечивает именно очищение от шума участков, расположенных внутри определённых областей изображения, не вызывая при этом размывания его краёв относятся:
1) направленные фильтры; один из методов предполагает использование линейного фильтра, симметричного относительно некоторой оси, а не точки. В этом случае при обработке каждого пикселя предпринимается попытка оценить направление границы изображения (если она имеется) и фильтр не допускает усреднения точек в направлении, поперечном границе.
2) составные фильтры; составной фильтр представляет собой развитие идеи направленного линейчатого фильтра. Этот вид фильтрации предусматривает в первую очередь применение к изображению фильтра нижних частот и вычисление градиента исходного изображения f(x,y). Эта процедура позволяет получить некоторое представление о расположении краёв изображения. Затем к изображению полученному в результате первого шага фильтрации, снова применяется фильтр, но его коэффициенты уже зависят от местоположения обрабатываемого участка на изображении и поэтому края изображения размываться не будут.
Если исходное изображение не сохранилось, то к изображению, подвергнутому фильтрации, можно применить фильтр верхних частот, коэффициентам которого при обработке участков изображения с большим значением градиента присваиваются большие значения, а при обработке остальной части изображения - малые. Эта процедура должна обеспечить восстановление значений элементов исходного изображение на участках с высоким значением градиента.
Если же исходное изображение имеется, то целесообразно воспользоваться фильтром низких частот.
3) фильтры приближения функций; принцип действия фильтров этого типа основывается на замене исходного изображения f(x,y) локальной оценкой одной из её статистических характеристик. Для определения соответствующих статистических характеристик необходимо разбить изображение на участки с некоторыми фиксированными размерами. В простейшем варианте этого метода на каждом из выделенных участков изображения оцениваются среднее значение и дисперсия функции f(x,y). Если значение дисперсии оказывается ниже заданного порога. то значения f(x,y) заменяются её средним. В противном случае соответствующий участок разбивается на более мелкие и процедура повторяется. Таким способом обеспечивается выделение краёв.
Вместо оценивания среднего значения можно обратиться к приближению f(x,y) некоторой гладкой функцией и переходить к разбиению участка на более мелкие, если ошибка приближения оказывается чрезмерно большой.
Сегментация
Сегментация позволяет выделить участки изображения, кажущиеся наблюдателю однородными; эта операция обеспечивает разбиение изображения на области одинакового вида.
Анализ сцен представляет собой задачу, связанную с сегментацией. Его цель состоит в получении описания изображения на некотором языке.
Разделение по порогу - этот метод предусматривает сопоставление значений яркости каждого пикселя с пороговым, в результате чего соответствующий пиксель зачисляется в одну из двух групп в зависимости от того, превышает значение яркости пороговое или нет. Выбор значения порога обычно производится по гистограмме.
Зрительное восприятие очень чувствительно к изменениям уровней яркости и в меньшей степени - к их абсолютным значениям.
Методы обнаружения границ и распределения по порогу основаны на определении разности значений яркости пикселей. Метод выделения областей путём их наращивания предусматривает поиск групп пикселей с близкими значениями яркости.
В простейшем варианте этот метод предусматривает выбор пикселя и изучение смежных с ним пикселей для проверки близости значений яркости сопоставляемых пикселей. Если значения яркости оказываются близкими, то соответствующие пиксели зачисляются в одну группу, чтобы сформировать область. В этом случае область формируется в результате сращивания отдельных пикселей.
В более эффективных вариантах метода в качестве отправной точки используются не отдельные пиксели, а разбиение изображения на ряд небольших областей. Затем каждая область проверяется на однородность (равномерность освещённости), и если результат проверки оказывается отрицательным, то соответствующая область разбивается на более мелкие участки. Процесс продолжается до тех пор, пока все выделенные области не выдержат проверку на однородность. После этого начинается формирование областей при помощи наращивания небольших областей, а не пикселей.
Проекции
В обработке изображений термином проекция обычно обозначают отображение изображения в сигнал, значения которого представляют собой суммы значений яркости элементов изображения, расположенных вдоль определённых направлений.
Восстановление тоновых изображений по их проекциям является одним из наиболее известных способов применения ЭВМ в медицине.
Этот метод может быть распространён и на восстановление трёхмерных объектов по их двухмерным проекциям при помощи объединения последовательности поперечных сечений.
Восстанавливаемым объектом, как правило, является какой-либо из органов человека.
Структуры данных
При решении прикладных задач, требующих базы изобразительных данных и длительного хранения изображений, приходится сопоставлять новые изображения со старыми или просматривать группы изображений, отыскивая на них определённые признаки. Таким образом, в дополнение к проблемам, связанным с объёмами памяти, необходимой для хранения изображений. проблемы могут возникать и при обращении к памяти.
Человеку нетрудно сосредоточить внимание на каких-то определённых частях двумерного изображения, тогда как ЭВМ вынуждена обрабатывать его вслепую. Следовательно, очень важны алгоритмы обхода изображения. В дискретном случае обход изображения соответствует обходу некоторой дискретной сетки, которую можно интерпретировать как некоторый граф: его вершинами служат пиксели, а рёбра связывают вершины, соответствующие смежным пикселям.
Обход связанного графа - простая процедура, если она осуществляется следующим образом: выбирается начальная точка, затем осуществляется переход в смежную точку, причём все пройденные позиции отмечаются. Если смежных точек несколько, то выбирается одна из них и в неё осуществляется переход, при этом остальные точки игнорируются - они могут быть пройдены позже при продолжении обхода.
Подходящей структурой для хранения этих точек является стек, представляющий собой массив, элементы которого накапливаются в процессе обхода, а при обращении алгоритма к массиву элементы из массива удаляются. Основной принцип действия стека состоит в том, что элемент, введённый в него последним, удаляется из него первым.
Стек представляет собой структуру данных, хорошо подходящую для обхода области, однако существуют задачи, в которых необходимо удалять элементы из массива в той же последовательности, в какой они в него вводились. Соответствующая структура данных называется очередью.
Пирамиды или тетрарные деревья представляют собой структуру данных, которая широко используется и в машинной графике, и в обработке изображений. Её применение даёт наилучшие результаты в случаях, когда изображение представляет собой некоторую квадратную матрицу А, размеры которой определяются некоторой степенью числа 2-(2n). Матрицу А можно разбить на 4 квадратные матрицы: А0 , А1, А2, А3, размеры которых в два раза меньше размеров матрицы А. Процесс такого разбиения можно рекурсивно повторить n раз до тех пор, пока не будет достигнут уровень выделения одного пикселя.
Корень дерева соответствует изображению в целом, листья - отдельным пикселям, а все остальные вершины характеризуются степенью исхода, равной четырём. Дерево такого вида называется деревом четвёртой степени или тетрарным деревом.
Бинарные деревья представляют собой полезную модификацию тетрарных деревьев и обладают рядом достоинств:
1) меньшая вариация чёткости от уровня к уровню. Если в случае тетрарного дерева разрешающая способность при каждом переходе учетверяется, то в случае бинарного каждый переход приводит лишь к её удваиванию. Поскольку в обоих случаях общий объём остаётся одним и тем же, бинарное дерево позволяет быстрее построить более точное изображение;
2) возможность использования соотношения между средним значением и отклонениями, что позволяет передавать не больше битов, чем содержится в исходном изображении.
Сжатие и выборочный просмотр изображений отражают всего лишь два из наиболее типичных способов использования тетрарных (бинарных) деревьев. Ещё одну важную область применения эта структура данных нашла в сегментации изображений.
Алгоритмы расщепления-слияния представляют собой развитие этого подхода. Процесс начинается с изучения вершин (квадратов) некоторого промежуточного уровня тетрарного дерева. Если некоторый квадрат оказывается неоднородным, то он заменяется четырьмя собственными подквадратами (процедура расщепления). С другой стороны, если оказывается, что четыре квадрата образуют однородный квадратный участок изображения, то они и заменяются этим участком - квадратом (процедура слияния). В данном случае дерево используется не для преобразования изображения, а для управления обходом. Но при реализации этой структуры данных неизбежно возникает проблема, связанная с хранением квадратов с переменными размерами.
Если число битов, необходимое для представления характеристик квадрата равно m и число квадратов равно N, то в целом необходимые затраты памяти будут составлять N(3n+m). Значение коэффициента сжатия:
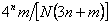
Так как правило n=m=8, то для представления изображения с переменной чёткостью требуется меньший объём памяти, если число квадратов составляет менее ¼ числа пикселей.
Изображение класса 2 можно закодировать, представив его последовательностью длин участков определённого цвета или яркости. Подобную информацию выгоднее всего хранить лишь для первого участка каждой строки, а для остальных участков следует запоминать только отклонения длины и яркости (или код цвета). Такой способ представления изображения часто называют кодирование с переменной длиной кодовой последовательности (КПДКП).
Этот способ можно использовать и для кодирования изображений класса 1, при этом диапазоны изменения значений уровней яркости аппроксимируются их средним значением. Размер памяти, необходимой для хранения значений длин и яркостей, составляет I(n+m), на одну строку, где I - число интервалов в строке, а n и m обозначают те же величины, что и выше. При типичном числе уровней серого тона, равном 8, экономия памяти достигается, если I меньше числа пикселей, составляющих строку, разделенного на 2. То есть использование кодирования с переменной длиной кодовой последовательности может привести к существенной экономии памяти.
Иконографические представления довольно сложны, однако являются наиболее эффективным средством хранения и преобразования изображений. При этом способе представления предполагается, что изображение разделяется на подызображения, которыми могут служить произвольные страницы, квадраты тетрарного дерева, области, полученные в результате сегментации изображения и т.д. Однако, вместо того чтобы хранить все изображения, некоторые из них заменяют меткой-описанием.
Двухуровневые изображения
Вместо выделения контура области, можно применить к ней процедуру прореживания, обеспечивающую построение остова области - фигуру типа человечка из спичек, кривые и сегменты которого отражают форму изучаемой области.
Если линию можно дискретизировать лишь одним способом (путём деления её на интервалы), то в двухмерном случае возможности безграничны. Приходится задавать не только размеры сетки выборки, но и её вид.
С практической точки зрения главной проблемой при дискретизации изображений класса 2 является сохранение формы областей. Для обеспечения последнего необходимо, чтобы связанные области непрерывного изображения оставались связанными на дискретном изображении. Необходимость сохранения связности автоматически порождает проблемы, относящиеся к топологии.
Поскольку при обработке изображений обычно встречается топология, индуцированная эвклидовой метрикой, то топологическая эквивалентность означает существование такого взаимно-однозначного отображения, при котором точки, расположенные вблизи друг от друга, отображаются в точки, расположенные вблизи друг от друга и наоборот. То есть область, в которой имеется дыра, не может быть топологически эквивалентна области, не имеющей дыры, поскольку соответствующее преобразование потребовало бы проведения разреза.
Когда говорят о дискретных изображениях, обычно имеют в виду восстановленные изображения. I - исходное изображение; каждому пикселю в процессе дискретизации присваивается тот цвет, в который окрашен центр соответствующей ячейки сетки выборки. В таком случае новое изображение J можно получить, заполняя каждый элемент (ячейку) воспроизведения изображения тем цветом, в который окрашен соответствующий пиксель.
Условие совместимости
Изображение класса 2 и сетка выборки с квадратными элементами называются совместимыми при выполнении следующих двух условий:
1) существует такое число, где h - длина стороны элемента сетки выборки, что для каждой граничной точки каждой области R заданного цвета найдётся окружность С диаметром d, касающаяся границы и полностью лежащая внутри области R;
2) то же самое справедливо и для дополнения области R.
Это условие совместимости задаёт нижние границы для ширины всех областей и кривизны их контуров. Так, в частности, не допускается наличие углов.
Дискретизация, при которой выполняется условие совместимости, обеспечивает сохранение формы.
Контуром или к-контуром связанного множества пикселей R называется множество всех пикселей из R, каждый из которых имеет, по меньшей мере, одного н-соседа, расположенного вне R; н-контуром множества R называется множество всех пикселей из R, каждый из которых имеет, по меньшей мере, одного соседа, расположенного вне R.
Обход пикселей контура можно осуществлять в соответствии с маршрутом, причём для такого обхода всегла можно использовать некоторый замкнутый маршрут. Процедура построения контура заканчивается, когда очередным пикселом, осматриваемым в процессе обхода, оказывается начальный.
Множество пикселей R называется полной областью, если оно содержит более четырёх пикселей, его к-контур является простым маршрутом и разность множества и его контура является н-связной.
То есть область является полной, если сетка дискретизации достаточно "точна" для того, чтобы ни одна из границ не раздваивалась.
Кривой или линейчатой областью на дискретной сетке называется такое множество пикселей, все элементы которого принадлежат контуру множества.
Ко-соседями пикселя, принадлежащего контуру С, называют пиксели, являющиеся для этого пикселя предыдущим и следующим элементом при обходе.
Пиксель называется кратным при выполнении одного или нескольких из следующих условий:
- данный пиксель просматривается более одного раза в процессе построения контура;
- данный пиксель не имеет соседей во внутренней части соответствующей области;
- данный пиксель имеет, по меньшей мере, одного н-соседа, который принадлежит контуру, не не является его Ко-соседом.
Анализ формы объектов представляет собой одну из основных задач распознавания образов.
Воспользовавшись определением через отсутствие некоторых признаков, можно указать, что форма представляет собой информацию, содержащуюся в двухуровневом изображении и не учитывающую цвет соответствующих областей.
Можно выделить два подхода к распознаванию формы объектов. При использовании первого человек рассматривает объект в целом и принимает решение, исходя из его общей структуры. При другом подходе исследуется контур силуэта: обычно отыскиваются углы, выступы, впадины и другие точки с высокими значениями кривизны.
Анализ контура может проводиться несколькими способами. Простейшая методология предусматривает получение несложного представления контура, например, в цепном коде. При использовании более развитой методологии контур аппроксимируется участками гладких кривых (например, В-сплайнами). Последнее предпочтительно в случаях, когда данные зашумлены, а также при использовании признаков, отражающих особенности значительной части контура.
Первый подход более уместен при работе с данными, отличающимися низким уровнем шума, и использовании локальных признаков. Широкое применение аппроксимации многоугольниками объясняется не только связанной с ней возможностью обнаруживать максимумы кривизны, но и тем, что её реализация оказывается проще реализации других методов построения кривых по точкам.
Многие алгоритмы, применяемые в распознавании образов, предусматривают вычисление интеграла по площади некоторой области, для чего они должны быть снабжены информацией о внутренней части области (в сущности, речь идёт о преобразовании изображения класса 3 в изображение класса 2).
Методы заполнения контура можно различать, исходя из того, какой принцип применяется в них для установления принадлежности точки внутренней части многоугольника. В некоторых алгоритмах используется проверка на чётность, в других - критерий связности.
1. Алгоритмы заполнения области, использующие проверку на чётность, основываются на том, что произвольная прямая пересекает любую замкнутую кривую (типа контура некоторой области) чётное число раз.
2. Заполнение области по критерию связности предполагает, что помимо контура задана некоторая точка, расположенная внутри области (затравка). В таком случае совершается обход плоскости, целью которого является обнаружение всех пикселей, достижимых из затравочной точки без пересечения контура.
Результаты применения алгоритмов прореживания могут явится основой соответствующего структурного анализа. В общем случае в результате структурного анализа должны быть определены элементарные блоки, из которых строится объект, силуэт которого задаётся как часть изображения класса 2. Этот процесс можно выполнять непосредственно при помощи разбиения объекта на ряд непроизводных объектов простой формы. Подобный путь требует значительных затрат вычислительных ресурсов. Аналогичных результатов, но с меньшими затратами можно достичь, обратившись к анализу остовов объектов.
Основным препятствием для применения структурных методов является отсутствие подходящих алгоритмов классификации.
Процедура прореживания в чистом виде не даёт полного решения задачи преобразования двухуровневых изображений в штриховые.
Построение по точкам и воспроизведение кривых
При решении одних прикладных задач допустимо представление кривой в виде последовательности пикселей, а при решении других предпочтительно задавать кривую с помощью математического выражения.
Отыскание кривой, проходящей через заданное множество точек, составляет задачу интерполирования, а отыскание кривой, проходящей вблизи заданного множества точек - задачи аппроксимации.
С математической точки зрения задачи интерполирования решать легче, однако при решении многих прикладных задач аппроксимация оказывается более практичной, так как точные значения обрабатываемых данных искажаются из-за наличия шума.
Компромиссным решением при выборе одного из этих методов служит выделение множества точек-ориентиров, которые могут быть определены пользователем в интерактивном режиме, и проведение кривой (или поверхности) вблизи этих точек.
Часто решающее значение при построении кривых по точкам приобретает выбор математического описания (функции).
Наибольшее распространение получили методы, предусматривающие использование кусочно-полиномиальных функций различных типов. При решении задач аппроксимации также следует уделять внимание выбору критерия, характеризующего качество приближения. Максимальное расстояние точек от кривой или поверхности представляется вполне разумным критерием, однако часто его использование порождает сложные вычислительные проблемы.
Для эффективного воспроизведения кривых необходимо, чтобы точки, составляющие отображение, порождались на одном из низших уровней, как правило, с помощью аппаратной части дисплея. Это обстоятельство ограничивает число классов кривых, поддающихся эффективному воспроизведению. Чаще мы имеем дело с кривыми двух классов: прямыми линиями и дугами окружностей.
Основным недостатком интерполирования с помощью многочленов являются существенные колебания, которые может претерпевать кривая, построенная между двумя точками. Причина подобного поведения интерполяционных многочленов заключается в том, что многочлен, в принципе, представляет собой сумму степенных функций х. Эти функции обладают тем свойством, что их значения на всём сегменте определяются значением на произвольном малом подсегменте. Подбирая коэффициент многочлена таким образом, чтобы сумма составляющих его функций принимала в нескольких точках искомые значения, мы не в состоянии контролировать значения отдельных членов в остальных точках. Поскольку значение каждого члена может быть достаточно велико, то появление значительных отклонений не должен являться неожиданным. То есть интерполирование с помощью многочленов имеет смысл только при сравнительно небольших сегментах.
Многочлены Безье
Этот класс многочленов применяется в интерактивных системах машинной графики для приближённого решения задач на построение кривых по точкам. Вместо непосредственного использования точек, представляющих обрабатываемые данные для задания многочлена при построении искомой кривой в интерактивном режиме определяется множество точек-ориентиров. Многочлены при этом задаются не в явном виде как y=p(x), а в параметрической форме:
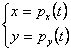
Содержательно многочлен Безье можно представить как некоторую намагниченную эластичную ленту, закреплённую в первой и последней точках; во всех остальных точках размещены магниты. Лента притягивается к каждой точке, причём чем выше напряжённость магнитного поля в точках (то есть чем выше их кратность), тем ближе будет притянута лента к ним. При стремлении кратности к ∞ многочлен Безье стремится к ломаной кривой, точками сопряжения для которой служат точки ориентиры.
Кривая, порождаемая многочленом Безье, обладает следующим интересным свойством: любую дугу, входящую в неё, также можно породить с помощью многочлена Безье. Это свойство оказывается полезным при определении поверхностей.
Влияние ошибок округления на воспроизведение кривых
Выбор надлежащего шага дискретизации кривой не является единственной проблемой, возникающей при попытках добиться хорошего воспроизведения. В общем случае математическое описание кривой, заданной на плоскости, может быть представлено или с помощью параметрического представления: x=X(t), y=Y(t), или уравнения f(x, y)=0.
Элементы структуры воспроизводимой кривой испытывают также влияние ошибок округления значений X(t) и Y(t). Все воспроизводимые изображения характеризуются некоторой конечной разрешающей способностью и для их получения каждый раз должен выбираться тот пиксель, координаты которого лежат ближе всего к вычисленным значениям координат, и воспроизводится должна точка именно с этими координатами, а не с координатами точно X(t) и Y(t).
При решении многих прикладных задач, предусматривающих построение кривых по точкам, может потребоваться внести изменения в одну часть кривой, не затрагивая другие. Многочлены свойством локальности не обладают, а многочлены Безье обладают лишь квазилокальностью. Изменение расположения или кратности одной из точек ориентиров требует пересчёта всей кривой, даже несмотря на то, что указанные изменения могут слабо влиять при удалении от соответствующей точки-ориентира. Кусочно-полиномиальные функции несомненно являются средством реализации локальных изменений.
В-сплайн - это сплайн, равный нулю на всех подсегментах, за исключением m+1.
Хотя сплайн-интерполяция обладает свойством локальности, построение, проводимое с учётом дополнительных степеней свободы, может оказать существенное воздействие на окончательный результат.
Сплайны между экспериментальными точками могут претерпевать колебания столь же резкие, как и те, что свойственны интерполяционным многочленам.
Использование сплайнов для построения кривых по точкам открывает ряд интересных возможностей, поскольку в этом случае можно ограничится заданием лишь точек-ориентиров, а не точек, действительно принадлежащих контуру.
Аппроксимация кривых. При построении кривой по точкам, осуществляемом в автоматическом режиме, субъективные критерии требуется заменить мерами близости, точно определёнными математически. Наиболее распространёнными из таких мер являются максимальная ошибка и суммарная квадратическая ошибка (СКО). Отклонение может измеряться либо по координате, либо по нормали к аппроксимирующей кривой.
Приближение и воспроизведение поверхностей
В обработке изображений и распознавании образов поверхности используются при анализе изображений, по крайней мере, двумя способами. Во-первых, изображение можно рассматривать как поверхность, используя значения яркости в качестве третьей координаты. во-вторых, можно рассматривать поверхности объектов, присутствующих на изображении.
Поверхности, как правило, слишком сложны для того, чтобы их можно было описать единственным уравнением во всей их области определения, и, следовательно, возникает потребность в кусочной аппроксимации поверхностей. Простейшими являются кусочно-линейные аппроксимации, в частности построенные посредством использования многогранника с треугольными гранями.
Во многих случаях число треугольников, необходимое для приемлемой аппроксимации, оказывается слишком большим и поэтому приходится обращаться к поверхностям высших порядков. Вследствие этого возникают проблемы представления таких кусочных поверхностей.
Одно из решений этой проблемы предусматривает задание на поверхности множества кривых и затем определение с помощью этих кривых интерполяционных конечных (участков) поверхностей, ограниченных соответствующими кривыми. Другой способ предусматривает использование точек-ориентиров или плоскостей-ориентиров.
В общем случае поверхность можно описывать с помощью одного из следующих уравнений:
явное: z=f(x,y)
алгебраическое: F(x,y,z)=0
параметрическое: x=X(u,v); y=Y(u,v); z=Z(u,v).
Если поверхность задана явным уравнением, то точки, в которых частные производные z по x и y обращаются в 0, называются особыми или стационарными.
Основная проблема, возникающая при воспроизведении изображений кривых, заключается в преобразовании математического описания соответствующей кривой в набор координат пикселей. Это единственная информация, которая необходима для воспроизведения плоской кривой. В случае же поверхности одних лишь координат (x,y,z) её точек явно недостаточно для того, чтобы воспроизвести её изображение. Известны два основных подхода: кодирование информации о высоте (координаты z) с помощью цвета и штриховка. Применение цветового кодирования приводит к воспроизведению контуров, что может быть полезно при решении некоторых прикладных задач, но не привлекательно на эстетически, ни информативно. Использование штриховки позволяет получать изображения лучшего качества, однако требует большего объёма вычислений. Если все поверхности являются плоскостями, то эффект штриховки можно получить, окрашивая в один цвет или воспроизводя в одном уровне серого тона проекцию каждой видимой плоскости. Иногда этого оказывается достаточно для создания впечатления глубины изображения. Ряд проблем, осложняющих воспроизведение неплоских поверхностей, возникает из-за необходимости работать с их проекциями на некоторую плоскость, и, следовательно, решать задачу разделения видимых и невидимых элементов - дело в том, что одни точки поверхности могу заслонять другие. В частности, очертания проекции конечного участка поверхности с замкнутой границей не всегда совпадают с проекцией этой границы.
При использовании растровых графических устройств для воспроизведения контуров достаточно просто установить некоторое соответствие между координатой z и цветом или уровнем серого тона. Если плотность выборки точек достаточно высока, то контуры, соответствующие постоянному значению z, будут представляться кривыми постоянной яркости. При использовании векторных графических устройств эта задача становится существенно более трудной, так как соответствующие кривые приходится прослеживать на воспроизводимой поверхности.
| 
